If we are told that a guy is 6’2” tall, or we dispense 20 liters of waters in toilet at one time, or somebody ate a dozen bananas, a perception about the quantity is immediately built in our minds. We immediately respond that ohh! 6’2” means really tall guy, or a dozen bananas at time means too much! But how would you respond to number of moles of oxygen entering into your body with each breath or molarity of sugar in lemonade you prepare? Perhaps our mind stop responding as quickly as previous answers. The primary reason is that we have never brought mole as a unit into our daily lives, and thus it became increasingly difficult to comprehend. Mole as a fundamental unit like meter, liter, second etc. is equally important.
With the revised definition of mole in 2018, its now a mere number with 6.022 x 10^23 entities representing it. No more confusion as 1/12 of carbon 12 and so on.. that has merely frightened high school students. I personally like the viewpoint of Nivaldo Tro who prefer to call a mole as a chemist's dozen. So if you can imagine a dozen bananas and a dozen pencils, a mole is no different, except for the fact that the numbers are too many but not 12.
With the revised definition of mole in 2018, its now a mere number with 6.022 x 10^23 entities representing it. No more confusion as 1/12 of carbon 12 and so on.. that has merely frightened high school students. I personally like the viewpoint of Nivaldo Tro who prefer to call a mole as a chemist's dozen. So if you can imagine a dozen bananas and a dozen pencils, a mole is no different, except for the fact that the numbers are too many but not 12.
It would be really good if you can bring the mole concept into real life, just like your have already brought other units. You have an estimate of time, (and can therefore imagine how much 1 hour means), you have estimate of distance (and can therefore imagine that how much 20 kilometers mean), but no clues about how many water molecules are present in your water bottle! May be we do not pay attention to it and never brought mole into real life,rather let it into the text books, which made the mole concept difficult.
Keep it simple
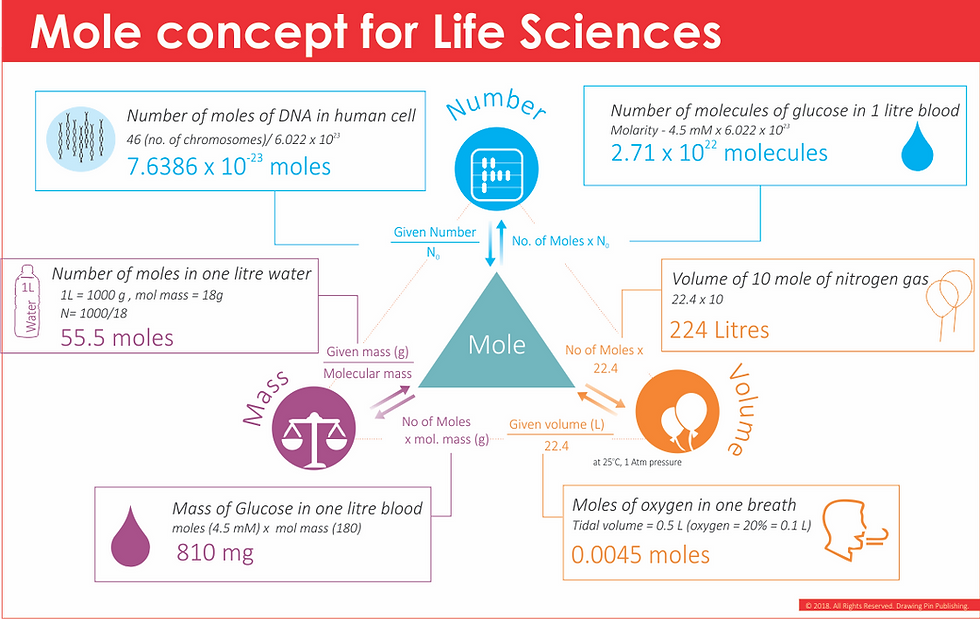
Understanding and calculations of mole can be understood better by keeping it simple. Rather than going into tough formula and tricky definition (old fashioned - like 1/12th of the weight of Carbon-12), it is okay to calculate the number of moles from the relations provided by Avogadro's. Where, a mole of a substance has a weight (in grams) equal to its molecular weight, i.e. 58.5 g sodium chloride (two large spoon) is one mole, 18 gram water (one spoonful) is one mole, 80 gram (half a small bowl) sugar is one mole. Although for gases, as it is difficult to estimate the mass, we measure volume,but volume also can change, so we fixed temperature and pressure conditions for gases and based on Gay Lussacs law, Avogadro's law it was determined that 22.4 liters of any gas has one mole.
Love triangle of mole concept
For further simplifying calculations keep the love triangle of mole handy with you all the times. I call it the love triangle as it helps you to love mole concept and make your life easier in solving mole based problems. Another small trick to calculate the number of moles is remember the word GK (general knowledge), where G represents GIVEN and K represents KNOWN. So, if you want to calculate the number of moles of anything divide given quantity by known quantity, i.e. given weight by molecular weight, given number by Avogadro's number and given volume by fixed volume (22.4), figure above shows the love triangle for mole concept. So one liter water bottle (that contains 1 Kg of water), will have (1000/18 = 55.5), 55.5 moles of water or 3.342 x 10^25 molecules of water or 3.342 x 10^25 atoms of oxygen and 6.68 x 10^25 atoms of hydrogen.
I wish, that you would try to bring mole concept into real life and the calculations will then become as obvious as imagine a dozen bananas. (read the complete published article here)
Comments